In the early 20th century, most computer code was written in binary and later in Assembly language, which was a tedious task for humans. From a modern perspective, can you imagine how difficult it would be to write code in Assembly, or even harder, to debug and maintain it? For this reason, people came up with the idea of creating human-readable ways of programming computers, and thus, high-level programming languages were born (yes, even C is a high-level programming language in that sense).
But as we know, the only language our computers speak is binary, so creating a translator that can translate our code to the computer's language was necessary. Thus, the first compilers were born. The main idea of compilation is to translate human-readable code into binary. Along the way, compilers became more powerful and incorporated many other features, primarily code optimization and debugging. Therefore, the main topic of this post will be to explain as simply as possible what happens under the hood and how nice, human-written code is transformed into "ugly" machine-readable code. Disclaimer before we start: everything that I say is a generalization of the compilation process, and none of the steps happen exactly as I say they do, simply because there are hundreds of languages with their ways of compilation. So I will just try to give a high-level overview of the ideas behind it.
The compilation process can be broken down into two main parts: the front-end and the back-end. The front-end includes steps like lexical analysis, syntax analysis, semantic analysis (which sometimes is not considered a separate step but rather part of syntax analysis), and intermediate code generation (the last one is also not always present because some compilers completely skip that step and are happy with whatever output syntax/semantic analysis provided). The backend, on the other hand, consists of code generation and code optimization. The main difference between the front-end and the back-end is that the former is a set of machine-independent operations, and the latter is machine-dependent. Before I talk more in-depth about each step, I want to give an example of pseudocode that we will use to simplify the whole process.
If Temperature <= 0 Then
Description = "Freezing"
End If
You will soon see how much work should be done to compile even such simple code.
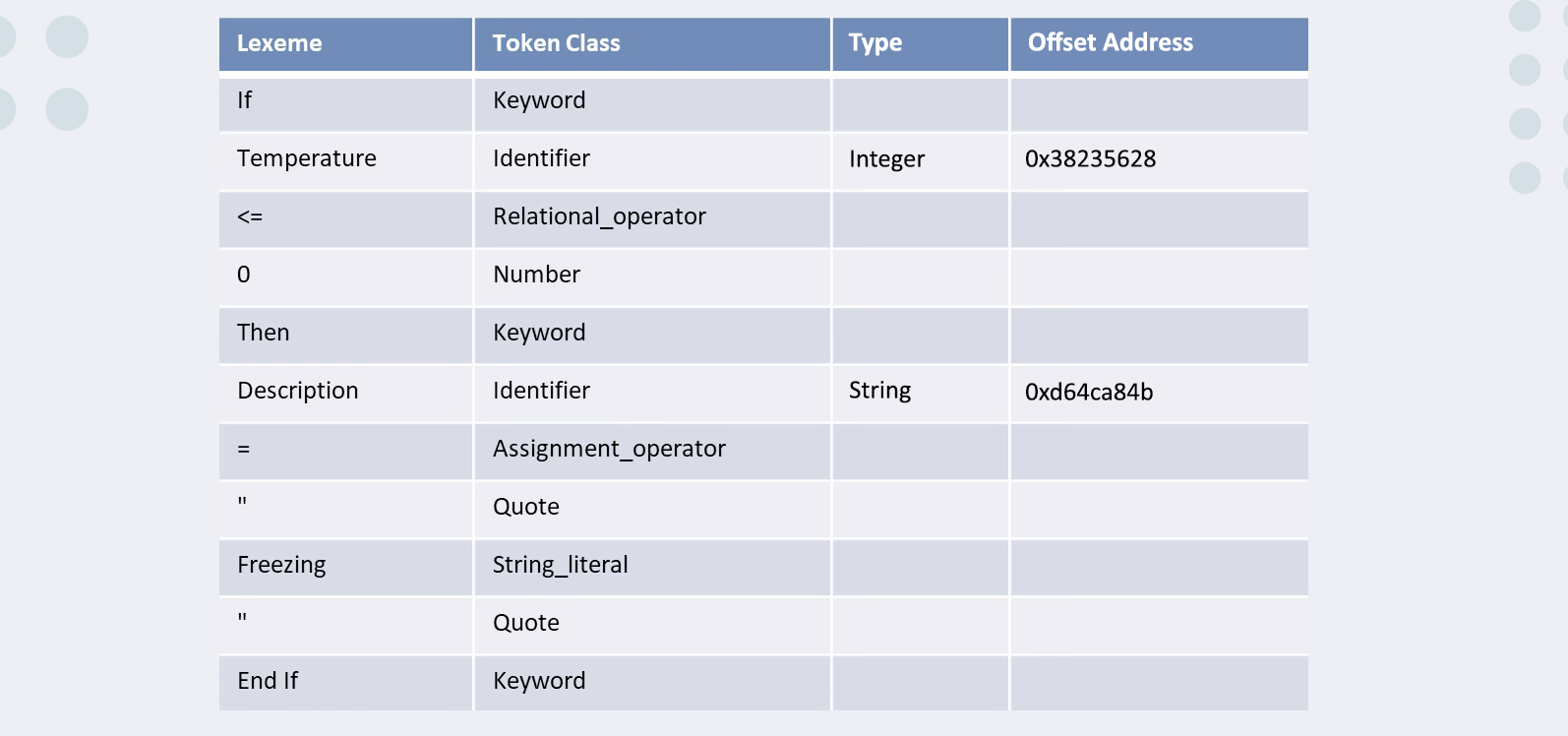
Lexical analysis is the first step of the compilation process. Lexical analysis is performed by a special program called a lexer. The lexer's main purpose is to determine the meaning of individual words in the source code. What does "determine meaning" mean? It's easier than it sounds. The lexer should identify what type each word is, for example, whether it is a keyword for a particular language or just a variable name. The lexer reads the source file character by character until it finds a word, also called a lexeme if we want to be more precise and sound smarter. In the majority of cases, lexemes are separated by whitespace, which includes spaces, tabs, line breaks, etc. But in some programming languages, whitespace also has meaning, for example, in Python where tabs define scope. The lexer creates tokens from lexemes found in the source code and saves those tokens in a symbol table. What is a token? Or a symbol table? For simplicity, we can imagine a token as a pair of two strings. On the left side, we have the lexeme, and on the right side, we have the lexeme type. But those tokens are not stored just as a pair of words. In most cases, tokens contain far more information about the lexeme aside from its type. For example, the exact location in the source file, which will be useful for debugging purposes. As for the symbol table, we will talk about it more in-depth soon.
Now you might ask, "Okay, but how does the lexer identify each lexeme and give it a proper label?" Good question. There are two main ways of doing that: regular expressions and tables that are prepopulated with language-specific keywords. The list below shows what tokens will look like for our pseudo code example.
[Keyword:If]
[Identifier:Temperature]
[Relational operator:<=]
[Number:0]
[Keyword:Then]
[Identifier:Description]
[Assignment operator:=]
[Quote:"]
[String literal:Freezing]
[Quote:"]
[Keyword:End If]
As you can see, the whole code is broken down into tokens, which will be stored in the symbol table as entries. Lexical analysis is not a complicated process, but it is also a very limited one in terms of error checking. At this stage, the only thing that can be properly checked is whether identifiers are named according to the rules, for example, variable names should not start with a digit but rather a character. (It cannot even check if we misspell a keyword because it will be understood as an identifier.) Now let's talk about symbol tables.
A symbol table is nothing but an in-memory data structure that is used to save information about each lexeme. For example, it can store information like the lexeme's data type (if applicable to a given programming language), location in memory (most often represented by an offset from the program's starting location), information about the lexeme's scope, and so on. Symbol tables are commonly implemented as hash tables, or in rare cases, as binary search trees. Those two choices are obvious because they provide O(1) for hash tables and O(logn) for BST insertion and search (or extremely fast speeds, in other words). We need such high speeds to make the compilation process as fast as possible because symbol tables are used extensively in almost every stage of compilation. Some compilers use more than one instance of a symbol table. For example, a compiler can create one symbol table for each scope and avoid the complexities required for scope validation. Here is the symbol table representation for our example.

Now we understand what symbol tables are, but why do we need them? Let's talk about the syntax analysis phase. As its name suggests, the syntax analysis phase is responsible for verifying that the code is syntactically valid, which means our code follows the rules provided by a specific programming language. For example, an if statement should be followed by parentheses or every case in a switch statement should end with a return or break keyword.

As you can see on the above image, many meaningless statements are valid for the syntax analysis stage, as long as they are not breaking any syntax rules. The program responsible for syntax analysis is also called a parser. The parser uses predefined grammar to check source code. But what is predefined grammar? It is a little bit more complex than it seems. It has foundations in theoretical computer science, or more specifically, in formal language theory. But for our purposes, grammar (or context-free grammar in our case, because it does not care about the meaning of the code yet) is nothing but a rule for constructing every valid string that is possible within the scope of our language. For example, valid Python code will break Java grammar rules, although Python code might make sense and have proper syntax for its own language. Java grammar rules are not the same as Python. You might ask, "How are those grammar rules defined, then?" That's a tricky question because it depends on who you ask. For mathematicians, grammar rules are expressed using special objects called automata, which come from automata theory. But understanding that notation requires a really good understanding of discrete mathematics and graphs specifically.
So to make grammar rules more accessible to people, a special notation called Backus-Naur form (BNF) was created. BNF is a handy way of describing grammar for anything and has a really simple syntax that is written in almost plain English.
<if then statement>::= if ( <expression> ) <statement>
<if then else statement>::= if ( <expression> ) <statement no short if> else <statement>
<if then else statement no short if> ::= if ( <expression> ) <statement no short if> else <statement no short if>
<switch statement> ::= switch ( <expression> ) <switch block>
<switch block> ::= { <switch block statement groups>? <switch labels>? }
<switch block statement groups> ::= <switch block statement group> | <switch block statement groups> <switch block statement group>
<switch block statement group> ::= <switch labels> <block statements>
<switch labels> ::= <switch label> | <switch labels> <switch label>
<switch label> ::= case <constant expression> : | default :
<while statement> ::= while ( <expression> ) <statement>
The sample above shows a small chunk of Java BNF. Now let's get back to our example and see how many lines of grammar rules we would need to create a language where we can only write if statements.
<if statement> ::= If <condition> Then <statement>
| If <condition> Then <statements> End If
| If <condition> Then <statements> Else <statements> End If
<condition> ::= <expression> <relational_operator> <expression>
<relational_operator> ::= <|>|<=|>=|=
<expression> ::= <expression> + <term> | <expression> - <term>|<term>
<term> ::= <term> * <factor>|<term>/<factor>|<factor>
<factor> ::= <identifier>|<number>|(<expression>)|<string_literal>
<statements> ::= <statement><statements>
<statement> ::= <assignment>|<if statement>|<for statement>...
<assignment> ::= <identifier> = <expression>
<identifier> ::= <letter>|<identifier><letter>|<identifier><digit>
<letter> ::= a|b|c|d|...|A|B|C|D|...
<digit>::=0|1|2|3|4|5|6|7|8|9
<number> ::= <integer>|<integer>.<integer>
<integer> ::= <digit>|<integer><digit>
<string_literal> ::= <quote><character><quote>|<quote><characters><quote>
<character> ::= <letter>|<digit>|...
<characters> ::= <character><characters>
<quote> ::= "
The photo above shows the grammar rules for our example, and we can see that some parts of the language are described recursively, which is quite logical. Let's take expressions as an example. Mathematical expressions can be infinite, so the recursive nature of the grammar supports that idea as well. For example, in the expression 3+(5+6), if we look closely, we can imagine (5+6) as another mathematical expression, so we can rewrite it as 3+expression, and recursion comes in handy once again. Another thing we might notice is that we are allowed to check wild conditions, like "omedia" > 5, because both sides of the relational operator > allow us to use either a string or a numerical value, and it is syntactically valid. But as previously mentioned, syntax analysis only cares about syntax, so we are cool with such anomalies (for now).
Now that we know how to describe grammar for other people so that they can understand it, let's consider how we can describe it for computers. How does a parser know anything about grammar rules? Let me introduce another in-memory data structure called a parse tree, also known as a concrete syntax tree. A parse tree is a special tree structure that is built according to the grammar rules provided by the programming language. This magical data structure is solely responsible for checking and validating syntax in source code.
To make things easier, let's return to our example and see how the parse tree will validate its syntax. First, let's look at the code itself. Each grammar rule is represented as a tree structure. To create one, we can simply take the declaration as the root node and add every part of its definition as a child node. If the definition itself is complex, we can recursively do the same for it and continue until we've done this for every grammar rule. As you'll see, almost every tree will be made up of subtrees, and some of them will be recursively described with pointers to other data structures to avoid infinite depth trees. Let's see the parse tree for our code:

This is a greatly simplified version because many of the nodes are completely omitted to save space. In reality, our tree would be much larger. Now that we have a parse tree, how do we check the code? It's easy! We ask the lexer or symbol table to give us tokens in the order they appeared in the code. Let's say we receive the 'if' token first. We can then go into our parse tree and try to put it in the appropriate node. We start from its children nodes and the first match is already valid, so the 'if' statement is valid here. We can then move on and ask for another token. Let's say we receive 'temperature.' It is an identifier, so we should traverse our parse tree, and if we go deep enough on the second child of the root node, it will lead us to the righteous path. We will find the appropriate leaf for our identifier. But let's say we receive another 'if' statement instead of an identifier. As you can see, no matter how deep we traverse the second child of our parse tree, we will never find a single leaf node where an 'if' statement can be inserted. Thus, the 'if' statement appeared where it was not valid for it to be. Syntax rules were broken, and now our compiler is angry and stops the compilation process altogether. That's a great simplification, but the idea is that every token is checked against the parse tree. If there is a leaf node valid for it, it is syntactically valid. If the parse tree can't find any place to store the token, it's invalid. Simple as that.
So we've talked about syntax and lexical analysis, but we have to admit that the only things we can check are identifier naming and syntax rules. That's simply not enough. We need another analysis step: semantic analysis. At this phase, most of the good stuff is done, such as checking for undeclared variables, multiple declarations in the same scope, accessing out-of-scope variables, data type mismatches, mismatched return values and function parameters, and so on. Semantic analysis introduces the most amount of checks in the analysis stages. But how does it do that? I think you've already guessed it - another data structure, this time with a cooler name: the abstract syntax tree (AST). A sibling of the parse tree, but the main difference between them is that the AST does not contain any grammar-specific nodes, but rather only tokens that were present in the code. It is much smaller in size and contains only useful information. However, an abstract syntax tree is not enough for validation - it needs help from its old pal, the symbol table, where every bit of useful information is stored for each node in the abstract syntax tree. Unfortunately, at this stage, validation has no unified algorithm because there are simply too many things to check. For that reason, each check is done separately using data provided by the symbol table. For example, if we want to check for data type mismatches, we take the token, take its value as well, and ask the symbol table to provide information about each token - specifically, what data types are they? If they match, we're happy. If they don't, it means our programmer was a JavaScript developer who had no idea that strings and integers are different things, and the compiler throws an error. If we want to check the scope for our variable, it's easy - we ask the symbol table to provide information about the scope. If we want to know whether or not a given variable was declared in this scope, it's again easy - we ask the symbol table to give us the exact moment (scope) when the variable was declared. So, you get the picture - semantic analysis is just reading syntactically checked code token after token and using information provided by the symbol table to check if the code makes sense.
So our code went through three different analysis stages, and the source code, once represented as simple text, is now represented as an AST. Some compilers are done with the frontend steps here and pass the AST to the backend for code generation and optimization. But there is one additional step left in the frontend which I want to talk about - intermediate code generation. The whole idea of it is to create machine-independent optimizations and move the code a little bit closer to machine-readable form (assembly code, for example).
Intermediate code generation breaks down code into elementary steps. At this point, we should remove nested blocks and complex arithmetic or logical operations - every statement must be simplified. The most frequently used method for this is TAC (three-address code), which implies that we must have at most one assignment and one operation on the left side of the assignment. To make it a little bit more clear, let's take a look at some examples of how a complex program block can be turned into TAC code.

Why is it useful, you might ask? First of all, complex code is now represented in small operations which resemble the way CPUs work. CPUs have no idea about while loops or conditional statements made up of six conditions - they need simple instructions to operate. But most importantly, it enables the ability to optimize code no matter where it will be run. For that kind of optimization, we need to break down the code even further. Now, the code is broken down into basic blocks - a basic block is a group of related operations that always occur together. In each block, we can start optimizing the code. For example, we can eliminate dead code, code duplication, and redundant mathematical operations. We can change the order of operations to make the most use of memory space and registers present in our CPU. We can also perform every mathematical operation in advance and change it to constant values to avoid calculations, hence avoiding additional overhead during runtime.

So, intermediate code generation creates an optimized representation of the code that we can now pass to the backend part, where it will undergo further machine-specific optimizations. Hence, we've reached the backend task: object code generation, which creates an executable file (or something close to it) from our intermediate code. Now, this stage is a little bit mysterious because many steps are dependent on the machine architecture, for example, what type of CPU the target machine uses. Is it RISC (Reduced Instruction Set Computer) or CISC (Complex Instruction Set Computer)? The former has fewer but faster operations, while the latter has a much larger set of operations. But no matter how different the target machines are, some problems that need to be solved are the same for each one of them. For example, instruction selection, which is nothing but matching CPU instructions to our instructions written in code. For example, when we said "goto" in our basic blocks, the chance is the CPU does not have a goto operation, but has its own counterpart. At this stage, every operation in a basic block should be mapped to appropriate counterparts in the CPU. The second is register allocation and assignment to ensure as optimal memory usage as possible and avoid collisions in the CPU. Instruction ordering is the next challenge - knowing which operation must be performed when. It might sound trivial when thinking about our example, but now imagine a multi-threaded program, and that simplicity goes away. There are many other things that must be done at this stage, and those tasks are not trivial to explain.
But, at the end of the day, what we need to understand is that object code generation is just nothing but translating our intermediate representation to machine-readable (or close to) form.

The photo above shows how code specific to some CPU will look like after this step. Our intermediate code will now be translated into assembly, which is one step away from being binary code. And if we get to this stage, turning assembly to binary is indeed a trivial task. We look for specific numeric codes for each CPU operation in the given CPU manufacturer manual, then we turn every address into the appropriate memory location, and voila! Every bit of assembly is now represented with numerical values. Now, we pass those numerical values to RAM, which delegates it to the CPU, and our lovely code that we wrote on a plastic keyboard is now in the realm of semiconductors and high and low voltages - i.e., it is being executed by our machine.

